자기주도형 학습을 위한 표준수학

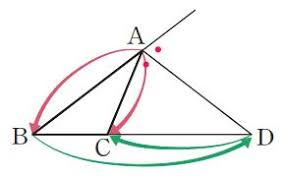
Geometry Quiz 2034 ♧     ♧     ♧     ♧     ♧     ♧ Hint 1  " 회전시켜서 평행이 되도록 한 이유를 잘 생각해 보세요  " Hint 2  " 평행선이 주어졌다면, 각의 크기들을 한번 알아볼까요? " Hint 3  " 이등변삼각형은 어디에 숨어 있을까요?  " ♧     ♧     ♧     ♧     ♧     ♧ Solution   & Answer  2034

삼각형 외각의 이등분선 정리 exterior angle bisector theorem "평행선과 닮음이 이렇게도 활용되네요! " " we can apply parallel lines & similarity to prove this!  " 삼각형 내각 의 이등분선 그리고   외각의 이등분선 정리 들과 그 증명 과정들은 중학과정 의 도형기하 단원 뿐만 아니라, 고등학교 및 대입수능 시험에서 복합유형의 응용문제 형태로 자주 등장하는 매우 중요한 내용입니다. 단순히 그 결과를 기억해 두고 사용하는 것도 중요하지만,  평행선의 성질과 닮음을 활용하는 그 증명과정들도 매우 중요 하니, 확실하게 공부해 두기 바랍니다. 내각 의 이등분선과  외각의 이등분선 정리를 별도로  꼼꼼하고  아주 쉽게    설명할 예정이니 ,  철저히 이해하고 응용력을 키워 두기 바랍니다 . ♧     ♧     ♧     ♧     ♧     ♧ 아래 그림과 같이 삼각형의 외각의 하나인  꼭지각  ∠ A   의 외각을  이등분한 선이 밑변  BC  의 연장선과 만난 교점을  D  라 할 때, 다음 변들의 길이의 비가 서로 같다는 정리입니다. AB  :  AC  =  BD  :  DC 왜 그럴까요? 다음 그림과 같이, 점  C  를 지나 외각의 이등분선인  AD  와 평행한 직선을 그어, 변  AB  와 만나는 점을  F  라고 해 볼까요? 위 그림에 빨간색 점들로 표시된 것과 같이 여러 각들의 크기가 서로 같네요? 초록색으로 표시된 두 평행선의 동위각이니까, ∠ EAD  =...

절대값 일차함수 linear absolute value functions " 절대값 그 래프부터  상위수학의 시작입니다 " " graphing absolute value functions  will lead you to the higher level mathematics " 함수의 그래프는 고등수학 미적분까지 이어지는 중고등수학의 가장 핵심적인 단원입니다 . 이 중에서도 ,  절대값 함수의 그래프는 구간을 나누어 생각해야 하고 ,  각각의 구간별 풀이는 교집합 ( ∩ ) 과 합집합 ( ∪ ) 의 개념을 논리적으로 정확하게 적용해야 하는  사고력 수학의 전형적인 유형 입니다 . 중고등 과정의 중급 및 심화문제에서 자주 등장하는 매우 중요한 유형이고 ,  함수 그래프에서도 많이 응용이 되는 개념이므로 ,  반드시 기본개념과 응용력을 철저히 익혀야 합니다 . ♧     ♧     ♧     ♧     ♧     ♧ 함수  y  = |  x  |  의 그래프는 어떻게 그려야 할까요 ? 절대값이 포함된 일차함수도 ,  앞에서 배웠던 절대값 방정식과 같이  절대값 안의 값이 양 (+)의 값 인지 음 ( – )의 값 인지에 따라 , 2  가지 경우로 나누어   그래프로 나타내는 것이 원칙입니다 . (A)     x  <  0...

약수의 개수와 합 the number and sum of factors " 아래 도표의 이 미지 를 기억하면  아주 쉬워요 " " just keep in mind the image of the table shown below " 양  (+)  의 약수의 개수와 그 합의 문제는 ,  중고등과정 수학에서 수시로 등장하는 중요한 유형입니다 . 중학 수학에서의 완전 제곱수 관련 문제나 고등과정에서의 수열의 합 등에서 ,  결합된 형태의 유형으로 자주 출제되고 있습니다 . 반드시 아래에서 설명되는  도표 이미지 를 기억해 두고 정확한 개념 ,  유도 과정과 응용력을 익혀서 ,  항상 활용할 수 있도록 해 두어야 합니다 . ♧     ♧     ♧     ♧     ♧     ♧ [ A ]  양 (+) 의 약수의 개수  (the number of positive factors) 예를 들어 , 12  의 양  (+)  의 약수는  1, 2, 3, 4, 6, 12  이지요 ?  그럼 이 숫자들은 어떤 원리에서 구해지는...