삼각형의 닮음(16) 삼각형 외각의 이등분선 정리
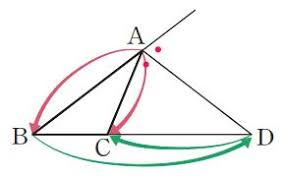
삼각형 외각의 이등분선 정리 exterior angle bisector theorem "평행선과 닮음이 이렇게도 활용되네요! " " we can apply parallel lines & similarity to prove this! " 삼각형 내각 의 이등분선 그리고 외각의 이등분선 정리 들과 그 증명 과정들은 중학과정 의 도형기하 단원 뿐만 아니라, 고등학교 및 대입수능 시험에서 복합유형의 응용문제 형태로 자주 등장하는 매우 중요한 내용입니다. 단순히 그 결과를 기억해 두고 사용하는 것도 중요하지만, 평행선의 성질과 닮음을 활용하는 그 증명과정들도 매우 중요 하니, 확실하게 공부해 두기 바랍니다. 내각 의 이등분선과 외각의 이등분선 정리를 별도로 꼼꼼하고 아주 쉽게 설명할 예정이니 , 철저히 이해하고 응용력을 키워 두기 바랍니다 . ♧ ♧ ♧ ♧ ♧ ♧ 아래 그림과 같이 삼각형의 외각의 하나인 꼭지각 ∠ A 의 외각을 이등분한 선이 밑변 BC 의 연장선과 만난 교점을 D 라 할 때, 다음 변들의 길이의 비가 서로 같다는 정리입니다. AB : AC = BD : DC 왜 그럴까요? 다음 그림과 같이, 점 C 를 지나 외각의 이등분선인 AD 와 평행한 직선을 그어, 변 AB 와 만나는 점을 F 라고 해 볼까요? 위 그림에 빨간색 점들로 표시된 것과 같이 여러 각들의 크기가 서로 같네요? 초록색으로 표시된 두 평행선의 동위각이니까, ∠ EAD =...

